本篇博客先介绍一些 naive 的方法来解决 BBO 问题,这样可以让大家了解到为什么DFO在实际中,如此受到欢迎。
两个缩写:
derivative free optimization (DFO) :无导数优化
black-box optimization (BBO) :黑箱优化
两者的两点区别:
(1)对于某些优化问题,可能存在导数,但获取或估计导数在计算上可能会很难。此类问题最好通过DFO解决,而不是BBO解决;
(2)BBO还包括研究用于解决问题的启发式方法或特用的方法;
优化问题:
m
i
n
{
f
(
x
)
,
x
∈
Ω
}
\begin{aligned} min\{f(x),x\in \Omega\} \end{aligned}
min{f(x),x∈Ω}?
即:优化目标是
f
(
x
)
f(x)
f(x),约束条件是
x
∈
Ω
x\in\Omega
x∈Ω。设
S
S
S是闭集
Ω
\Omega
Ω的可数紧集,则ES算法求解最优解的算法流程为:

看完流程可知,上述算法的实质就是“遍历”。。。。。
遍历所有解寻找最大的那个,因此,叫做 Exhaustive Search,而此时的优化求解的确没有用到导数,满足了DFO的要求。文中假设ES算法可以无休止地运行下去,故该算法的收敛性可得到证明,这里只给出收敛性成立的定理,不给出证明步骤,定理如下:
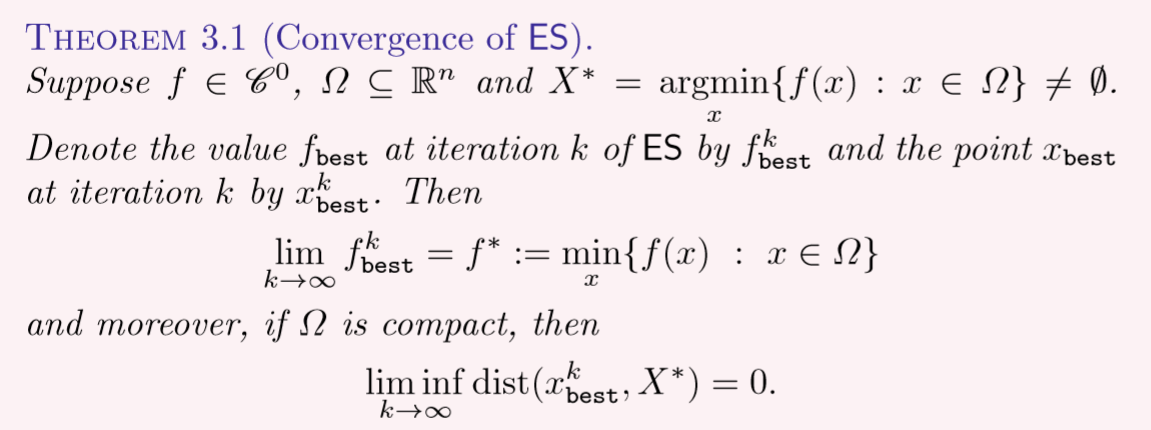
顺便提一句,在 R n R^n Rn中寻找一个可数的集合 S S S,那集合 S S S的规模可不小,准确地说是无穷个元素(因为他有可数个元素),也由此可知是没有办法在有限次叠代后终止ES算法的,因此ES算法不具备实用性,只存在于理论中。
上一节的ES算法对 Ω \Omega Ω没有要求,但当 Ω \Omega Ω是有界的集合时,则可使用本节的GE算法。
该算法的算法流程是:

看完流程可知,上述算法的实质就是“抽样”的思想,即:等距切分集合 Ω \Omega Ω为 p p p份后,再遍历。。。。。。
这样一来相比ES而言,至少是可行的,不再只是理论上可行而实际上无法求解的了,但是GS算法仍然需要庞大的计算搜索工作,实际中虽然可行,但是难以采用。最后,GS算法的收敛性证明及收敛性定理都省略,可参考原书。
CS算法是GS的改进,该算法的思想略有类似于梯度下降,其算法流程如下:

如果提供了约束集 Ω Ω Ω,则只要违反该约束,就可以通过将目标函数值设置为 + ∞ +\infty +∞再应用CS算法即可。
下图为CS算法再二维平面搜索过程的叠代实例,初始点为(2,2),初始步长为1,搜索方向为四个方向。第一次叠代搜索成功,寻找并得到了比当前值小的一组解。第二次叠代搜索失败,因此,步长减半,继续搜索。

对于n维问题,算法的每次迭代都精确地探索2n个方向。但是叠代需要有一个判定迭代终止的条件,这里的条件可以是步长小于某数值,或者叠代超过N次,或运行到明天早上8点停止等等。
说明:
(1)CS算法得到的是局部最优解,GS算法得到的是全局最优解;
(2)CS算法的收敛性问题:

(3)(待确定?) 根据上述收敛性可知,若目标函数是不可微函数或 f ( x ; d ) ≥ 0 f(x;d)\geq0 f(x;d)≥0时(尤其是是凸函数时,则任意点处都 ≥ 0 \geq0 ≥0),此时CS算法可能会失败;
可采用“拉丁超立方抽样(Latin hypercube sampling,LHS)”的方式,选取多组初始点。在统计抽样中,拉丁方阵是指每行、每列仅包含一个样本的方阵。拉丁超立方则是拉丁方阵在多维中的推广,每个与轴垂直的超平面最多含有一个样本。假设有N个变量(维度),可以将每个变量分为M个概率相同的区间。此时,可以选取M个满足拉丁超立方条件的样本点。需要注意的是,拉丁超立方抽样要求每个变量的分区数量M相同。不过,该方法并不要求当变量增加时样本数M同样增加。
LHS算法流程如下:

抽取案例如下图:

LHS的方式可以作为许多算法选取初始点的方案。
下表列出了后文待介绍的的高水平BBO算法:

(遗传算法等启发式类型的,我们不予介绍了)
