作为一个作业吧:想一下怎么定义state, action, reward;有了这些之后,TD learning, Q-learning, Monte Carlo都可以用了。如果假设知道transition model, (想一下如何定义),那么policy iteration, value iteration也可以用。
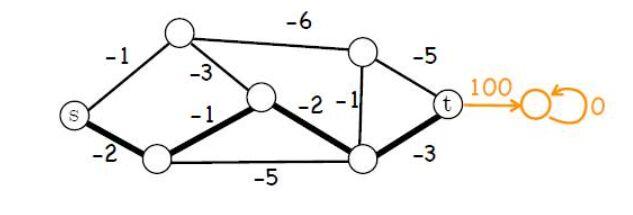
如果我们有节点、边、边的距离这样的图的全局信息,那么Dijkstra算法可以高效地找到最短路径。强化学习算法可以不用这些全局信息,而是用model free的方式,根据某个策略在图中不断采集本地信息,更新值函数,最终可以找到最短路径。Dijkstra算法在知道图的全局信息时,是最短路径的高效算法;而强化学习可以不依托于这些全局信息,比Dijkstra算法的适用面更广,是一般性的优化方法框架。
我记得有用强化学习搞组合优化的。最短路径问题其实已经被很好得解决了,我觉得你的重点应该放在路由上比较好,虽然感觉强化学习搞这种确定性问题没啥大优势。
如果路径是非常复杂的,且只能观察到局部的路径(有点像第一人称视角,而不是卫星视角),但每走一段路,你就会知道距离,经过若干次探索,可能就会到终点。
这里面可以抽象出来(S,A,R,Done),S就是你当前所处的位置,A就是你采取的行动(就是你往哪个方向走),R就是你走的距离,Done就是布尔值(代表是否到达终点)。
强化学习的优势就在于,你只需要去采样(S,A,R,Done),再定义合适的算法,就有可能把相对好的路径找出来,而无需将整个环境的模型建立出来。
这在现实是有一定意义的:很多东西都是黑箱,你可能无法了解它的内部结构,一是内部结构可能比较复杂,人们很容易认知过载,二是内部结构可能处于保密的要求而不公开,三就是以人类现在的科技水平可能无法认知……虽然内部结构未知、可以认为是个黑箱,但只要能够和它交互、有反馈的话,那么就可以采用强化学习的方法,虽然有可能找不到最优解,但应该可以找到相对优的解。
最短路径问题其实属于组合优化问题的一种,如果我们有节点、边、边的距离这样的图的全局信息,那么Dijkstra算法可以高效地找到最短路径。而常见的启发式算法有遗传算法,蚁群算法,模拟退火算法等,既然题主问的是用强化学习算法,这里我就不赘述了。附专栏和博文
图的最短路径算法及matlab实现(Dijkstra算法、Floyd算法、Bellman-Ford算法、Johnson 算法)https://zhuanlan.zhihu.com/p/107215125接下来我们来了解一下强化学习算法如何解决组合优化问题。
从广义上讲,组合优化问题涉及从有限的一组对象中找到“最佳”对象。在这种情况下,“最佳”是通过给定的评估函数来测量的,该函数将对象映射到某个分数或成本,目标是找到最低成本的对象。大多数实际中有趣的组合优化问题也非常困难,因为即使问题的大小只增加了一点,集合中的对象数量也会以极快的速度增加,导致穷举搜索不切实际。
例如常见的旅行商问题,假设我们有N个城市,我们的销售员必须全部访问它们。然而,在城市之间穿梭会产生一些费用,我们必须找到一种方案,在旅行到所有城市并返回起始城市过程中最大限度地减少总累积成本。
其抽象的数学模型与题主的问题接近。
鉴于题主应该已经有一定的基础,我们用一幅图和几个关键词来描述一下强化学习
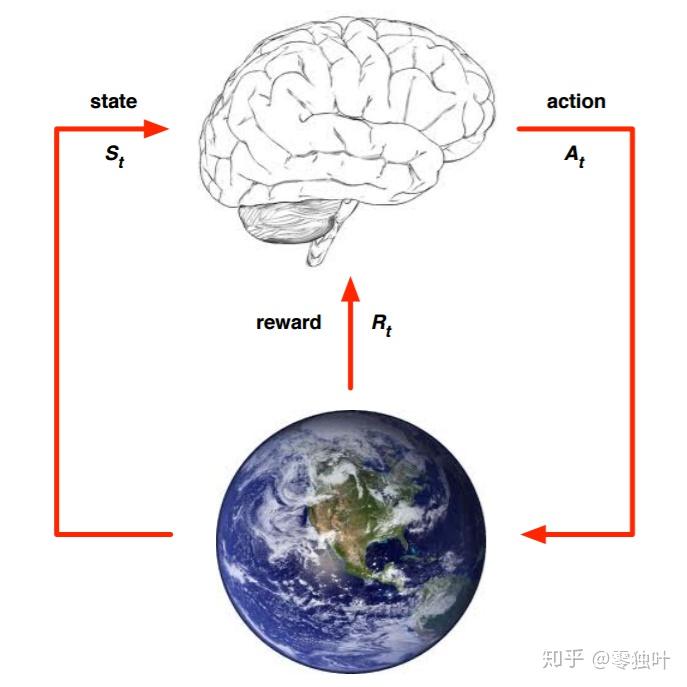
a.时序信息,在决定合适的行动时,需要考虑后续步骤
b.延后给出的奖励值(如:下棋最终的胜负)
c.交互与观察
组合优化问题大多数情况下都是涉及到决策顺序,即序列的决策问题,例如对于TSP问题就是决定以什么顺序访问每一个城市,而深度神经网络里边的递归神经网络恰好可以完成从一个序列到另一个序列的映射问题,因此可以借用递归神经网络来直接求解组合优化问题完全是一种可行的方案。另外一套方案就是采用强化学习,强化学习天生就是做序列决策用的,那么组合优化问题里边的序列决策问题完全也可以用强化学习来直接求解,其难点是怎么定义state, reward和action。
有了这些之后,TD learning, Q-learning, Monte Carlo都可以用了。如果假设知道transition model, 那么policy iteration, value iteration也可以用。
在大量搜索空间问题中寻找结构的探索是强化学习的一个重要而实用的研究方向。然而强化学习的许多批评者声称,到目前为止,它只用于解决游戏和简单的控制问题,并且将其迁移到现实世界的问题仍然很遥远。
值迭代就可以了
不用搞那么复杂。
