深度学习的优化函数

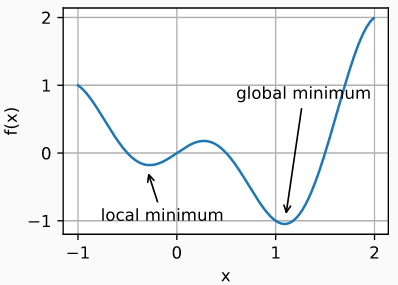
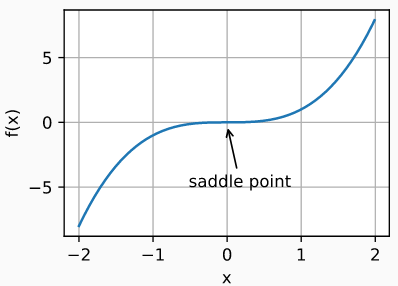
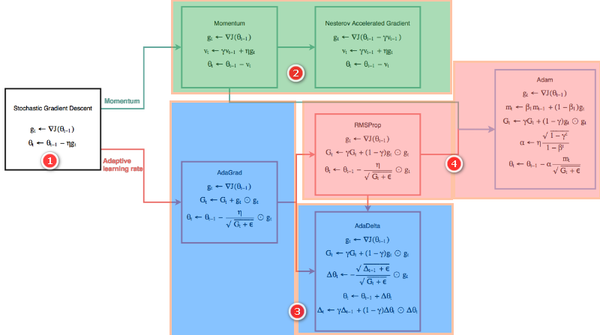
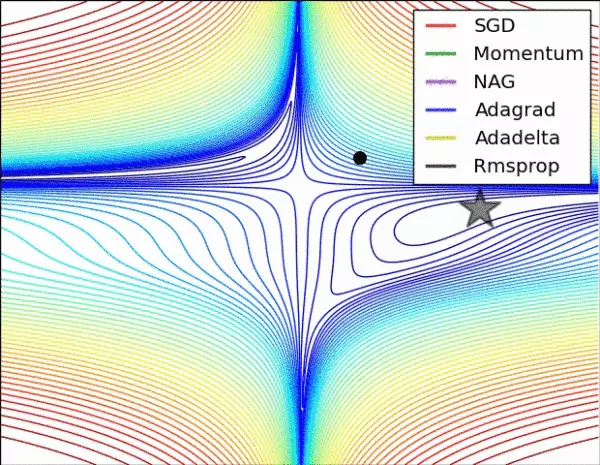
本文讲解了对神经网络进行参数更新的优化器，最基础的优化器是 w=w-rg，其中 w,r,g 表示参数、学习率和梯度，后面针对历史梯度、自适应学习率发展出不同的优化器，如 AdaGrad，Adam 等

• 

• 优化器在深度学习反向传播过程中，指引损失函数（目标函数）的各个参数往正确的方向进行适合的更新，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小
• 如何求最小值呢？对于凸函数可以直接求导可以找到最值，但是神经网络的优化本质上是一个非凸问题，而简单的基于梯度的优化器在实践中似乎总是能够解决这类问题

• 病态情况： 在优化凸函数的时候，会遇到 Hessian 矩阵(黑塞矩阵) 病态的情况。病态情况一般被认为广泛存在于神经网络的训练过程中，体现在随机梯度下降会“卡”在某些特殊的情况，此时即使很小的更新步长也会增加代价函数
• 局部最小值： 当优化问题的数值解接近局部最优值时，随着目标函数解的梯度接近或变为零，通过最终迭代获得的数值解可能仅使目标函数局部最优，而不是全局最优。只有一定程度的噪声可能会使参数超出局部最小值

  

• 鞍点 ： 指函数的所有梯度都消失但既不是全局最小值也不是局部最小值的任何位置

  

• 

• 1）基础版梯度下降法 (独立可变梯度)：梯度下降法 (Gradient descent, GD) 、批量梯度下降 (Batch Gradient Descent, BGD) 、小批量梯度下降 (Mini-Batch Gradient Descent, MBGD) 、随机梯度下降 (stochastic gradient descent, SGD)
• 2）加强版梯度下降法 (带一阶动量的梯度)：带动量 (Momentum)项、Nesterov 动量项
• 3）自适应学习率梯度下降法 (学习率与自身的梯度自相关)：AdaGrad AdaDelta
• 4）带二阶动态的梯度下降法：RMSProp、 Adam 、Nadam 、Adamax、RAdam
• 基于动量的优化器可以利用历史梯度参与参数更新；基于自适应学习率通过约束学习率达到快速收敛的目的

• 

• 如果是为了快速地获得原型，选择自适应算法，即 AdaGrad 、AdaDelta、RMSProp、Adam
• 如果是为了得到最好的结果，选择梯度下降算法，如小批量梯度下降(Mini-Batch Gradient Descent, MBGD)
• 如果你的数据偏小而且能够适应一次迭代，那么就可以选择诸如 LBFGS 这样的二阶技术。这是因为，二阶技术虽然速度非常快并且非常准确，但是只适用于数据偏小的情况。

• 即求取神经网络中输出相对于输入参数的变化率，以便确定神经网络中参数的调整方向及调整尺度， 并最终达到减少网络输出与真实结果的差异
• Pytorch 中为求导定义专门的包：autograd，如果使用 Variable 来定义神经网络参数，Variable 自动定义两个变量，其中 data 表示原始数据，grad 表示求导后的数据，也就是梯度
• 求取 out=mean ((x+2) _ (x+2) _ 3)的梯度，假设 ，则导数为： ，当 x=1 时，导数值为 4.5

    >>> import torch
    >>> from torch.autograd import Variable
    >>> x=Variable(torch.ones(2,2),requires_grad=True)
    >>> x,x.grad
    (tensor([[1., 1.],
            [1., 1.]], requires_grad=True), None)
    >>> y=x+2
    >>> y,y.grad # 正在访问非叶Tensor的grad属性y.grad。在backward()期间不会填充。如果确实希望为非叶张量填充.grad字段，请在非叶张量器上使用.retain_grad()
    (tensor([[3., 3.],
            [3., 3.]], grad_fn=), None)
    >>> z=y*y*3
    >>> z,z.grad
    (tensor([[27., 27.],
            [27., 27.]], grad_fn=), None)
    >>> z.backward() # RuntimeError: grad can be implicitly created only for scalar outputs
    >>> out=z.mean()
    >>> out,out.grad
    (tensor(27., grad_fn=), None)
    >>> out.backward()
    >>> x.grad,y.grad,z.grad
    (tensor([[4.5000, 4.5000],
            [4.5000, 4.5000]]), None, None)
  

• 采用整个训练集的数据来计算梯度，计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型
• Batch gradient descent 对于凸函数可以收敛到全局极小值，对于非凸函数可以收敛到局部极小值

    for i in range(nb_epochs):
      params_grad = evaluate_gradient(loss_function, data, params)
      params = params - learning_rate * params_grad
  

• 

• 不像批量梯度下降(Batch Gradient Descent, BGD)一次用所有数据计算梯度，SGD 每次更新时对每个样本进行梯度更新，对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本

  

• 可以看到 BGD 和 SGD 是两个极端，SGD 由于每次参数更新仅仅需要计算一个样本的梯度，训练速度很快，即使在样本量很大的情况下，可能只需要其中一部分样本就能迭代到最优解，由于每次迭代并不是都向着整体最优化方向，导致梯度下降的波动非常大

  

• 虽然看起来 SGD 波动非常大，会走很多弯路，但是对梯度的要求很低（计算梯度快），而且对于引入噪声，大量的理论和实践工作证明，只要噪声不是特别大，SGD 都能很好地收敛

• 小批量梯度下降法就是结合批量梯度下降(Batch Gradient Descent, BGD)和随机梯度下降(stochastic gradient descent, SGD) 的折中，对于含有个训练样本的数据集，每次参数更新，选择一个大小为
• Mini-batch gradient descent 不能保证很好的收敛性，学习速率 (learning rate)如果选择的太小，收敛速度会很慢，如果太大，损失函数就会在极小值处不停地震荡甚至偏离
• 对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点所有维度的梯度都接近于 0，SGD 很容易被困在这里
• Batch size 的选择参考：如何选择合理的 batch size?

• Online GD 于随机梯度下降(stochastic gradient descent, SGD) 、小批量梯度下降(Mini-Batch Gradient Descent, MBGD) 的区别在于，所有训练数据只用一次，然后丢弃。这样做的优点在于可预测最终模型的变化趋势
• Online GD 在互联网领域用的较多，比如搜索广告的点击率（CTR）预估模型，网民的点击行为会随着时间改变。用普通的 BGD 算法（每天更新一次）一方面耗时较长（需要对所有历史数据重新训练）；另一方面，无法及时反馈用户的点击行为迁移。而 Online GD 算法可以实时的依据网民的点击行为进行迁移

• 小批量梯度下降(Mini-Batch Gradient Descent, MBGD)用部分样本来近似全部样本，梯度相对于 batch size 为 1 更为准确，同时相比与使用全部样本，计算量减小，计算速度和收敛速度都会得到提升
• 为什么小批量的梯度下降更快，详细查看：为什么 10000 样本训练 1 次会比 100 样本训练 100 次收敛慢呢？

• 随机梯度下降(stochastic gradient descent, SGD) 在更新参数时对各个维度上梯度的放缩是一致的，并且在训练数据分布极不均很时训练效果很差，所以SGD 前期收敛慢
• 自适应优化算法 Adam、AdaGrad、RMSProp 等这些自适应的优化算法虽然可以在训练早期展现出快速的收敛速度，但其在测试集上的表现却会很快陷入停滞，并最终被 SGD 超过

• 

• 随机梯度下降(stochastic gradient descent, SGD) 和小批量梯度下降(Mini-Batch Gradient Descent, MBGD)算法都存在样本选择的随机性，因此含有较多的噪声，而 momentum 技术能解决上述噪声问题，借助类似指数加权平均(exponentially weighted averges) ，利用历史梯度参与参数更新。权重更新变为

  

• 其中 是动量项，取代之前的梯度，它是上一时刻的动量项与本次梯度值的加权平均值，按照时间展开，可知会按指数级累积以前的动量； 是学习率， 是动量系数
• 加入的这一项，可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡， 一般 γ 取值 0.9 左右
• 形象地说，动量法就像我们从山上推下一个球，在滚落过程中累积动量，速度越来越快，直到达到终极速度。在梯度更新过程中，对在梯度点处具有相同方向的维度，增大其动量项，对于在梯度点处改变方向的维度，减小其动量项

• 

• NAG 全称 Nesterov Accelerated Gradient，是在随机梯度下降 (SGD) 、带动量(Momentum)项的基础上的进一步改进，我们知道在时刻 t 的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。因此，NAG 不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，给动量项一个预知的能力，即梯度“多走一步”，可能跳出局部最优解

  

• 我们利用动量项更新参数，通过计算()得到参数未来位置的一个近似值，计算关于参数未来的近似位置的梯度，而不是关于当前参数 Wt 的梯度，这样 NAG 算法可以高效地求解
• 相对于 Momentum 的改进在于，NAG 算法相对于 Momentum 多了一个本次梯度相对上次梯度的变化量，这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息，NAG 算法才会比 Momentum 具有更快的收敛速度
• 形象地说，当球滚落的时候，一般是盲目地沿着某个斜率方向，结果并不一定能令人满意。于是我们希望有一个较为“智能”的球，能够自己判断下落的方向，这样在途中遇到斜率上升的时候能够知道减速

• 已知梯度下降法(Gradient descent, GD) 依赖于人工设定的学习率，如果设置过小，收敛太慢，而如果设置太大，可能导致算法那不收敛。和通过带动量(Momentum)项 加速收敛不同，AdaGrad 算法是通过约束学习率达到快速收敛的目的
• 对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些，AdaGrad 算法使用二阶动量感知参数的学习率，它是所有历史梯度的平方和，即

  

• 在更新参数时，通过乘以 ，就可以调整学习的尺度，前期较小的时候，较大，能够放大梯度；后期较大的时候，较小，能够约束梯度，适合处理稀疏梯度

  

• AdaGrad 算法依赖于人工设置一个全局学习率 η，设置过大的话，会使正则化项过于敏感，对梯度的调节过大，并且在训练的中后期，分母上梯度的平方的积累将会越来越大，使 gradient 趋向 0, 使得训练提前结束

• Adadelta 不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度，即只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值（指数移动平均值），这就避免了二阶动量持续累积、导致训练过程提前结束的问题了

  

• Adadelta 是对 AdaGrad 的改进，避免了长期累积梯度值所导致的学习率趋向于 0 的问题，同时去掉人工设置的全局学习率的依赖
• Adadelta 不依赖于全局学习率，在训练初、中期，加速效果理想化，训练后期，反复在局部最小值附近抖动

• RMSProp 算法修改了 AdaGrad 的梯度平方和累加为指数加权平均(exponentially weighted averges)，使得其在非凸设定下效果更好

  

• RMSProp 可以算作 AdaDelta 的一个特例，依然依赖于全局学习率。RMSProp 效果趋于 AdaGrad 和 Adadelta 之间，适合处理非平稳目标，适用于 RNN 的优化

• Adam 结合了前面方法的一阶动量和二阶动量对参数进行校正，本质上是带动量(Momentum)项的 RMSProp，其中一阶动量用于累积历史梯度，形成带动量(Momentum)项 ，二阶梯度用于累计梯度平方和，用于调整学习率

  

• 对一阶动量与二阶动量进行校正，并按下公式更新参数

  

• 可以看出，Adam 会设置 3 个超参数，即学习率 ，一次 momentum 系数，二次 momentum 系数
• Adam 算法的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定的范围，使参数比较平稳；对内存需求较小，适用于大多数非凸优化问题，尤其适合处理大数据集和高维空间问题

• 是 Adam 的一种变体，此方法对学习率的上限提供了一个更简单的范围

  >>> import torch.optim as optim
  >>> optim.Adamax(model.parameters(),lr=0.002,beta_1=0.9,beta_2=0.999,epsilon=1e-08)
  

• Nadam 是融合 Nesterov 动量项的 Adam ，对学习率有了更强的约束，同时对梯度的更新也有更直接的影响
• 一般而言，在使用带动量的 RMSProp 或 Adam 的问题上，使用 Nadam 可以取得更好的结果

• AMSGrad 是一个随机梯度下降优化方法，它试图解决基于 Adam 的优化器的收敛问题。AMSGrad 使用最大化过去平方梯度来更新参数，而不是使用指数平均，这样就降低了指数衰减平均，造成重要历史信息快速丢失的影响

  

• 是当前参数的梯度，为一阶矩估计的指数衰减率，是二阶矩估计的指数衰减率，前者控制一阶矩估计，后者控制二阶矩估计，从上面的公式可以看出，参数更新公式与 Adam 没有啥区别，但是求有区别

• AdaBound 算法训练速度比肩 Adam，性能媲美 SGD。随机梯度下降(stochastic gradient descent, SGD) 现在后期调优时还是经常使用到，但 SGD 的问题是前期收敛速度慢，自适应优化算法 Adam、AdaGrad、RMSProp 等这些自适应的优化算法虽然可以在训练早期展现出快速的收敛速度，但其在测试集上的表现却会很快陷入停滞，并最终被 SGD 超过
• AdaBound 对学习率进行动态裁剪，在这一设置下，在训练早期由于上下界对学习率的影响很小，算法更加接近于 Adam；而随着时间增长裁减区间越来越收紧，模型的学习率逐渐趋于稳定，在末期更加贴近于 SGD

  

• 把学习率限定在之间，其中是一个非递减函数，从 0 逐渐的收敛到 α，而是一个非递增函数，从 ∞ 逐渐收敛到 α , 在这种设置下，AdaBound 在最开始表现的像 Adam，因为最开始学习率的边界对更新公式影响很小，渐渐的表现的像 SGD+momentum，因为学习率逐渐被限制住了

• AdamW 本质上就是在损失函数里面加入了 L2 正则化，然后计算梯度和更新参数的时候都需要考虑这个正则项

  

• 权重衰减和 Adam 算法一起效果不佳，如果要一起使用，建议使用 AdamW

• 

• 一种兼具 Adam 和随机梯度下降(stochastic gradient descent, SGD) 两者之美的新优化器 ，收敛速度快，还很鲁棒
• 试图解决的问题是：自适应学习率优化器（如 Adam）需要学习率预热(warm-up)操作，否则就会陷入糟糕的局部最优。但是 warm-up 操作针对不同数据集需要手动调整，非常麻烦
• RAdam 使用了基于实际方差的整流函数进行“启发式 warm-up”，直到数据的方差稳定下来。通过这样做，避免了需要手动 warm-up，并且训练会自动稳定。一旦方差稳定下来，RAdam 基本上在训练的剩余阶段就会退化成 Adam 甚至等同于 SGD

• Lookahead 是一种梯度下降优化器，它迭代的更新两个权重集合，”fast”和”slow”。直观地说，该算法通过向前看由另一个优化器生成的快速权值序列来选择搜索方向。 梯度下降的时候，走几步会退回来检查是否方向正确。避免突然掉入局部最低点
• Fast weights： 它是由内循环优化器（inner-loop）生成的 k 次序列权重；这里的优化器就是原有的优化器，如 SGD，Adam 等均可；其优化方法与原优化器并没有区别，例如给定优化器 A，目标函数 L，当前训练 mini-batch 样本 d，这里会将该轮循环的 k 次权重，用序列都保存下来
• Slow Weights： 在每轮内循环结束后，根据本轮的 k 次权重，计算等到 Slow Weights；这里采用的是指数移动平均（exponential moving average, EMA）算法来计算，最终模型使用的参数也是慢更新（Slow Weights）那一套，因此快更新（Fast Weights）相当于做了一系列实验，然后慢更新再根据实验结果选一个比较好的方向，这有点类似 Nesterov Momentum 的思想

• 根据链式法则，如果每一层神经元对上一层的输出的梯度乘上权重结果都小于 1 的话，那么即使这个结果是 0.99，在经过足够多层传播之后，误差对输入层的梯度会趋于 0
• 当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习

• 根据链式法则，如果每一层神经元对上一层的输出的梯度乘上权重结果都大于 1 的话，那么即使这个结果是 1.01，在经过足够多层传播之后，误差对输入层的梯度会趋于无穷

• 深层网络导致浅层网络可能出现梯度消失或梯度爆炸
• 饱和激活函数导致梯度传播趋向 0，可能出现梯度消失
• 梯度消失和梯度爆炸本质上是一样的，都是因为网络层数太深而引发的梯度反向传播中的连乘效应

• 使用 Relu 、Leaky-ReLU 、elu 等不饱和激活函数
• 使用 批规范化(Batch Normalization,BN)
• 使用 ResNet 结构
• 逐层训练+ finetunning ： 每次训练一层隐藏层节点，将上一层隐藏层的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，这就是逐层预训练
• 梯度裁剪 (gradient clipping)
• 梯度正则化(regularization)： 检查网络权重的大小，并惩罚产生较大权重值的损失函数

• 在应用梯度值之前先设置其上限。梯度裁剪有助于确保数值稳定性以及防止梯度爆炸

• 

• 从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多

• 速度慢： 计算量大，训练非常慢
• 稳定性： 二阶方法能更快求高精度的解，同样对数据本身要的精度也会相应的变高，这就会导致稳定性上的问题
• 二阶方法能够更快地求得更高精度的解，这在浅层模型是有益的，而在神经网络这类深层模型中对参数的精度要求不高，甚至不高的精度对模型还有益处，能够提高模型的泛化能力

本文使用 Zhihu On VSCode 创作并发布