近来刚开始非凸领域的研究,亟需了解当下主流的算法,但稍作搜索后未找到心水的资料。因此花了几周的时间将目前的成果整理成思维导图,希望对同行有些用处。
新人学习,想必有很多疏漏,希望各位能人能够不吝留言赐教。感谢!
凸优化是机器学习中一个重要的问题,针对凸优化问题的算法已有许多优秀的研究成果,对于非凸优化的问题这几年也开始成为主流。方便起见,以下将凸优化与非凸优化算法统称为优化算法。
目录:
Part 1 优化算法分类:根据方法的基本原理分为6类
Part 2 各优化算法适用的问题类型:指出各算法适用于什么样的优化问题
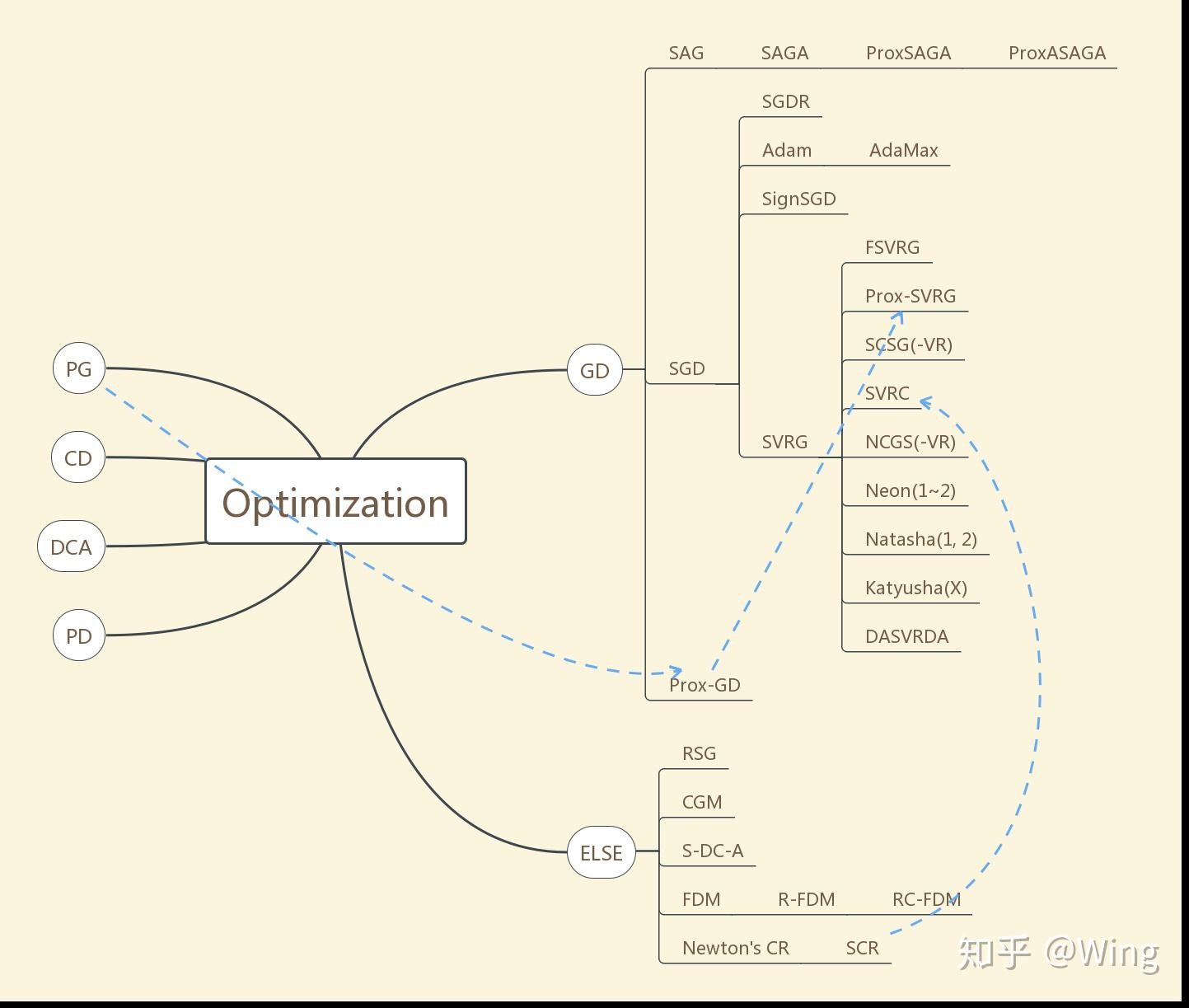
总体来看,主流的优化算法可分为五类,ELSE是相对小众的方法,因找到的论文较少,归在了一类。
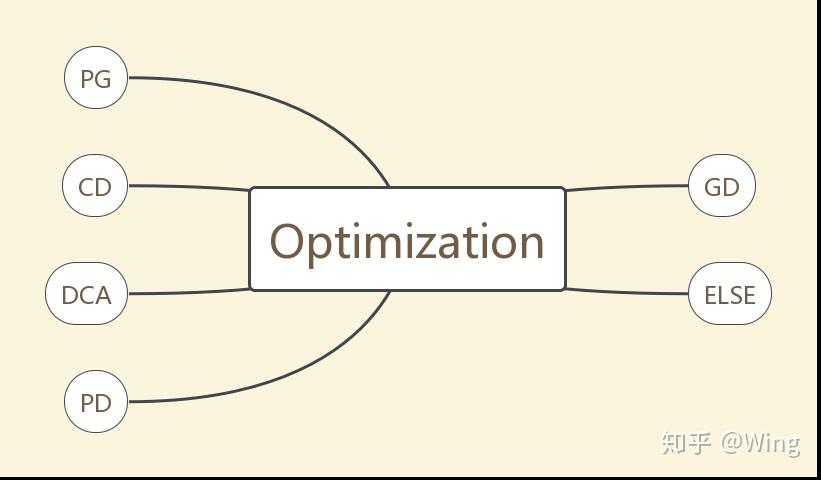
GD: gradient descent
PG: proximal gradient
CD: coordinate descent
DCA: dual coordinate ascent
PD: primal-dual
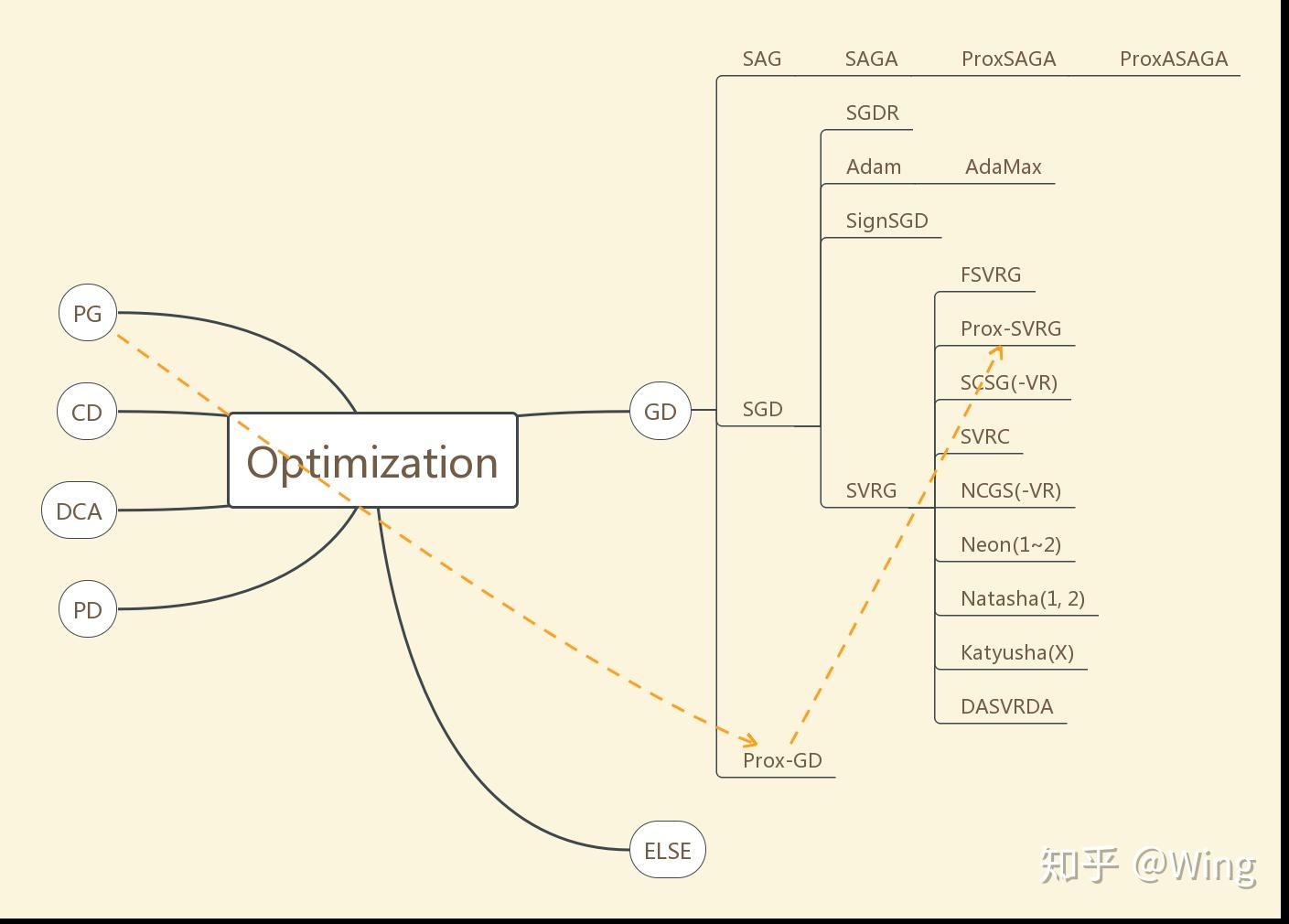
SAG: stochastic averaging gradient
ProxSAGA: proximal SAGA
ProxASAGA: proximal asynchronous SAGA
SGDR: SGD with warm restarting
FSVRG: fast SVRG
SVRC: SVR Cubic Regularization
NCGS: Non-convex Conditional Gradient Sliding
Neon: NEgative-curvature-Originated-from-Noise
DASVRDA: Doubly Accelerated SVR dual averaging
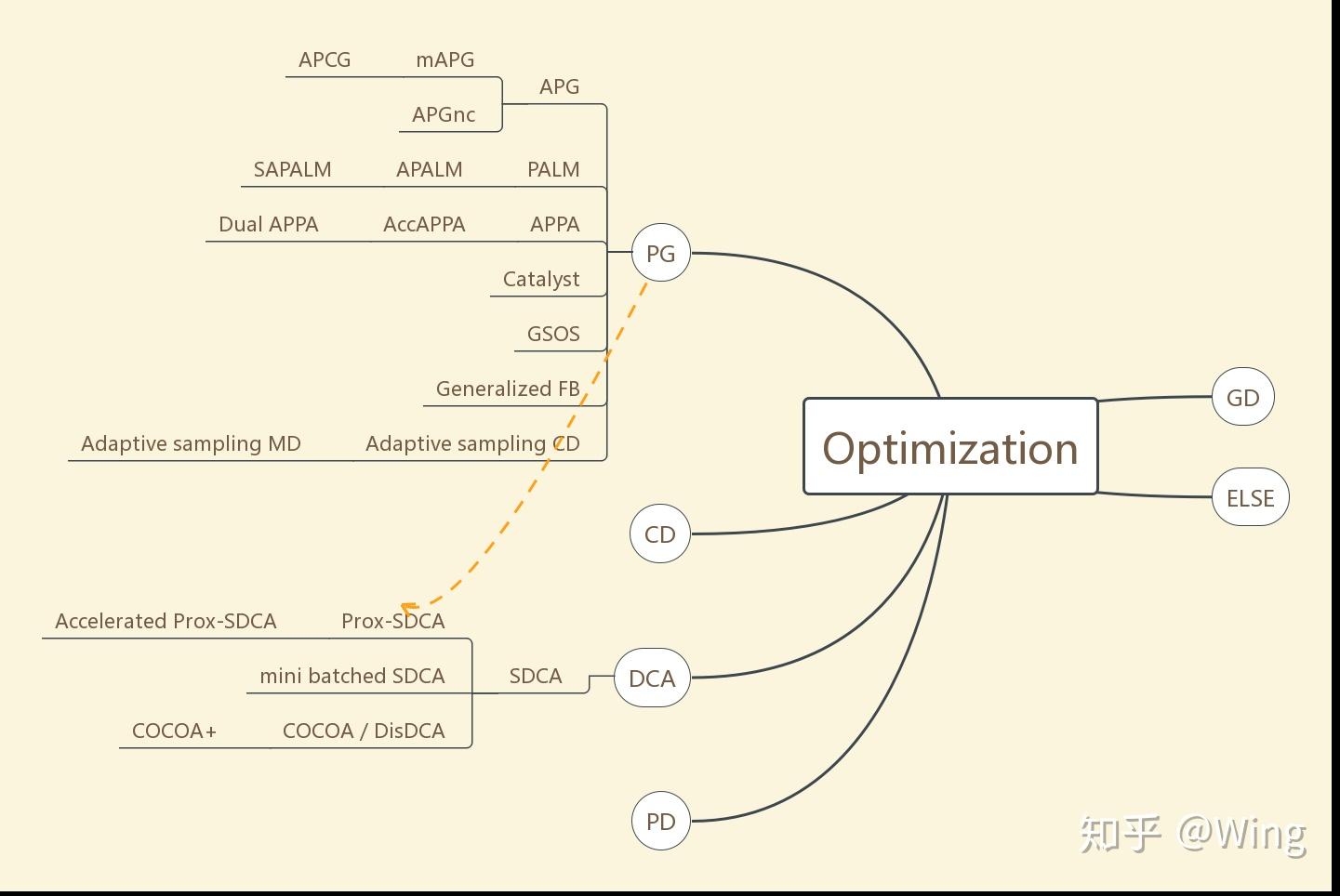
APG: accelerated proximal gradient
mAPG: monotone APG
APGnc: APG non-convex problem
APCG: accelerated proximal coordinate gradient
PALM: proximal alternating linearized minimization
SAPALM: stochastic asynchronous PALM
PPA: proximal point algorithm
APPA: Approximate PPA
GSOS: Gauss-Seidel operator splitting
FB: forward-backward
MD: mirrored descent
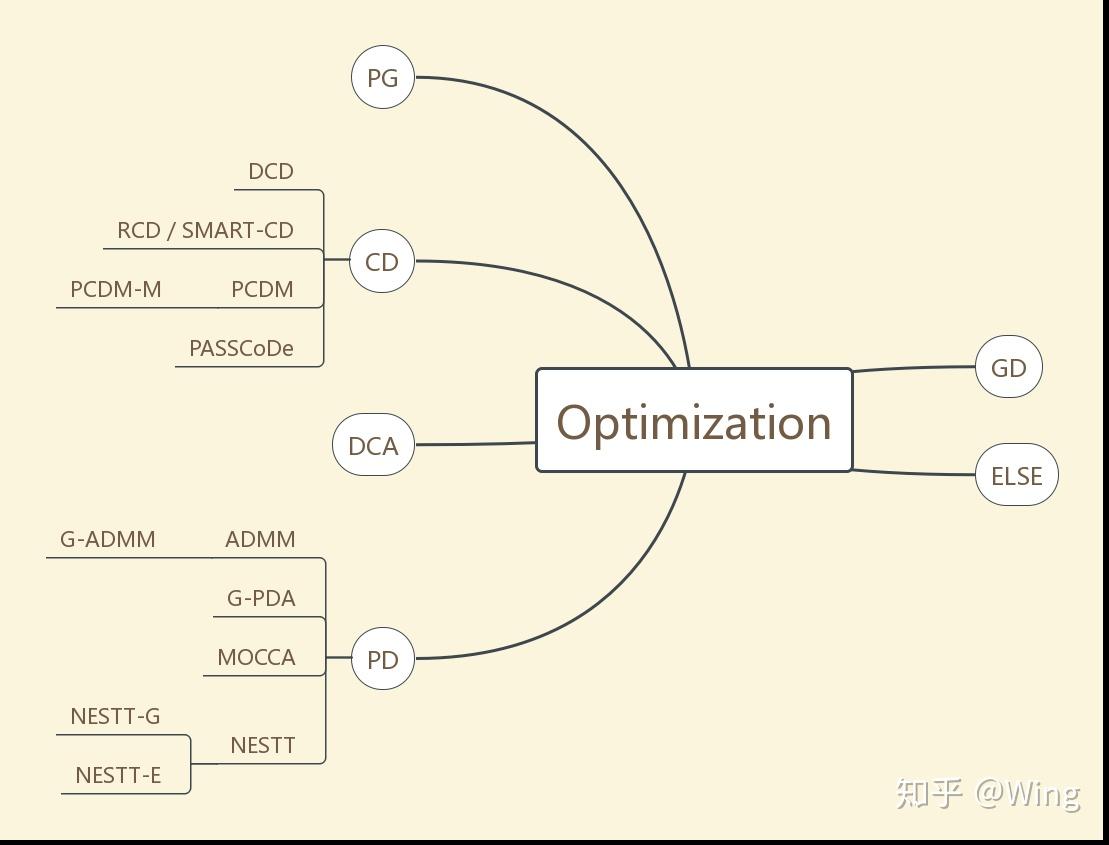
DCD: dual CD
RCD: randomized CD
SMART-CD: SMooth, Accelrate, Randomize The Coordinate Descent
PCDM: parallel CD method
PASSCoDe: Parallel ASynchronous Stochastic dual COordinate DEscent
G-ADMM: gradient ADMM
G-PDA: gradient primal-dual algorithm
NESTT-G: Non-convEx primal-dual SpliTTing-Gradient
NESTT-E: Non-convEx primal-dual SpliTTing-Exact
RSG: Restarted SubGradient
CGM: conditional gradient method
S-DC-A: stochastic difference of convex functions algorithm
FDM: feasible descent method
RC-FDM: randomized coordinate-wise FDM
SCR: sub-sampled cubic regularization
排除一些明显交叉学科的论文,基本上机器学习中的优化问题可以归纳为以下五类:
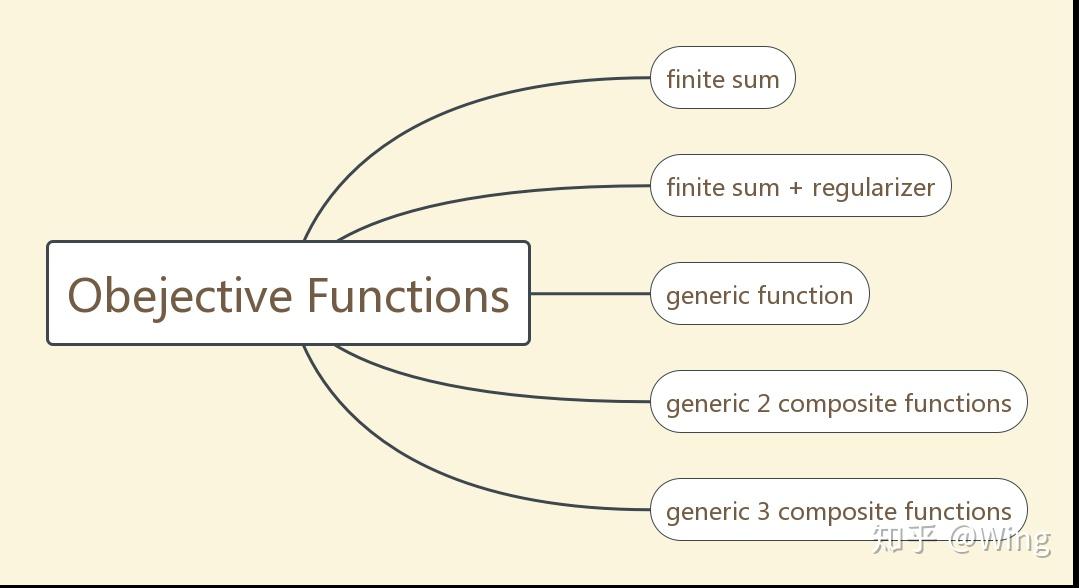
从图7开始,阅读的正确打开方式:算法名称-对目标函数作的基本假设
E.g.:
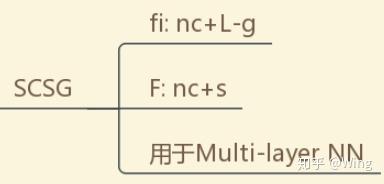
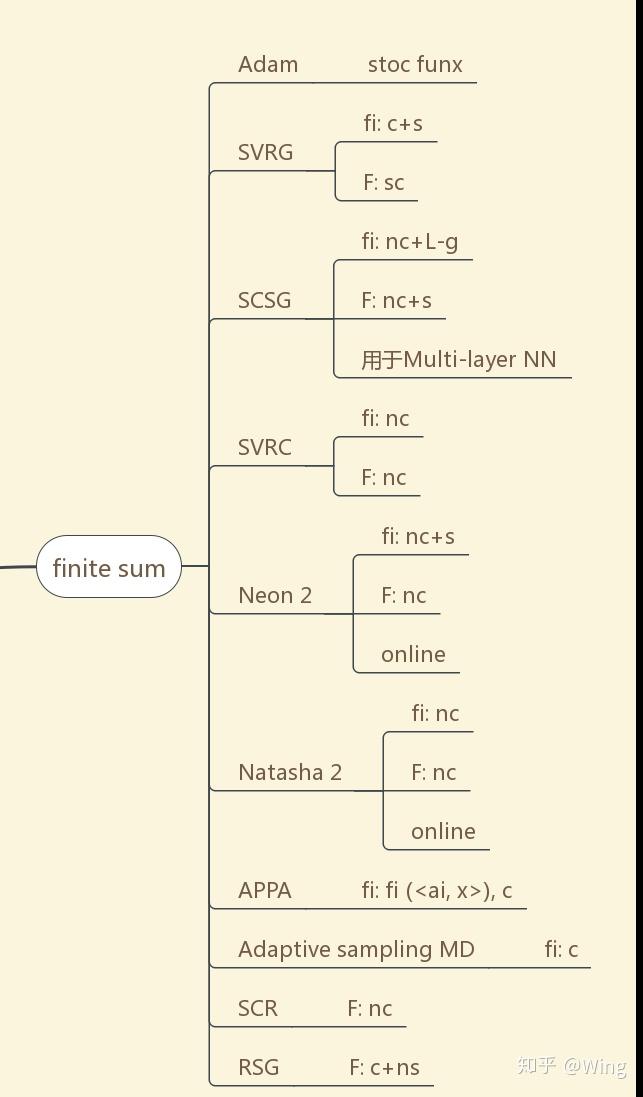
c+s: convex + smooth
nc + ns: non-convex + non-smooth
sc: strongly-convex
nc+L-g: non-convex + Lipschitz gradient continuous
nc+L: non-convex + Lipschitz continuous
c / nc: convex / non-convex
fi (<ai, x>):
phi:
square reg:
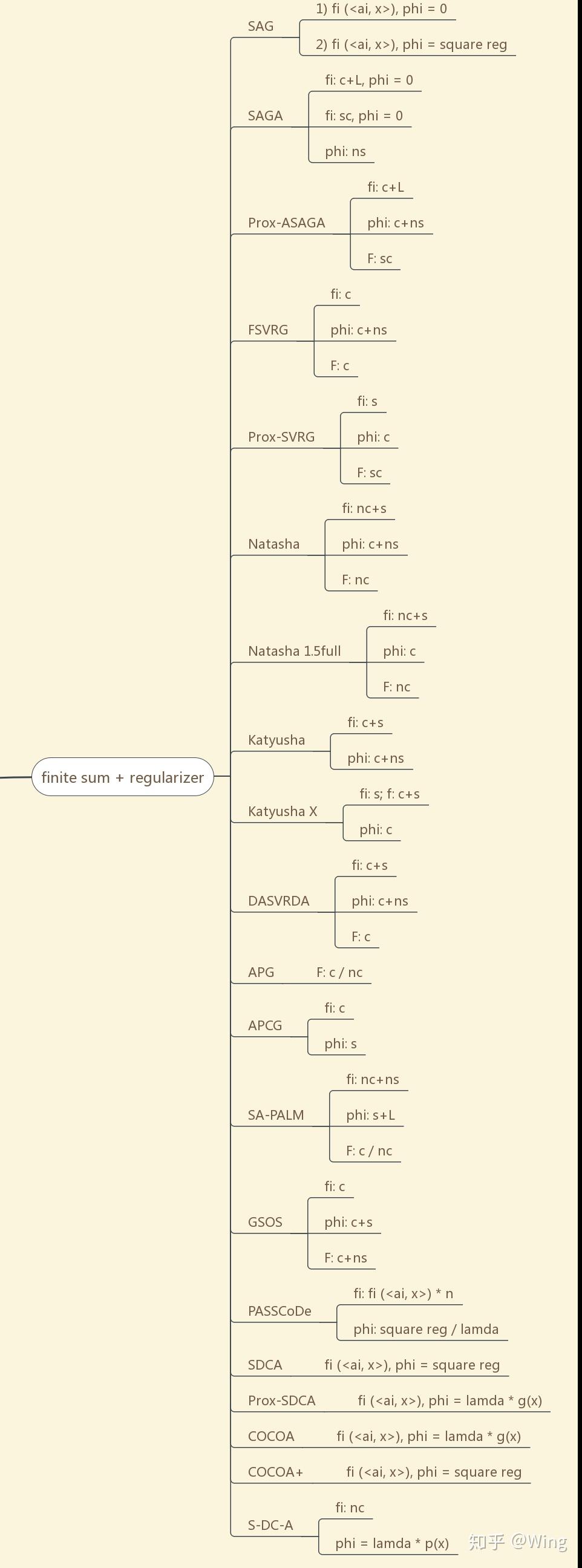
注:
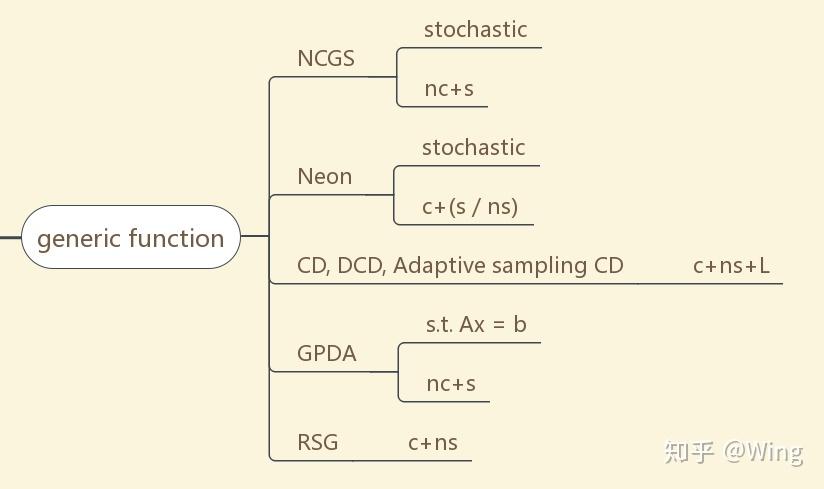
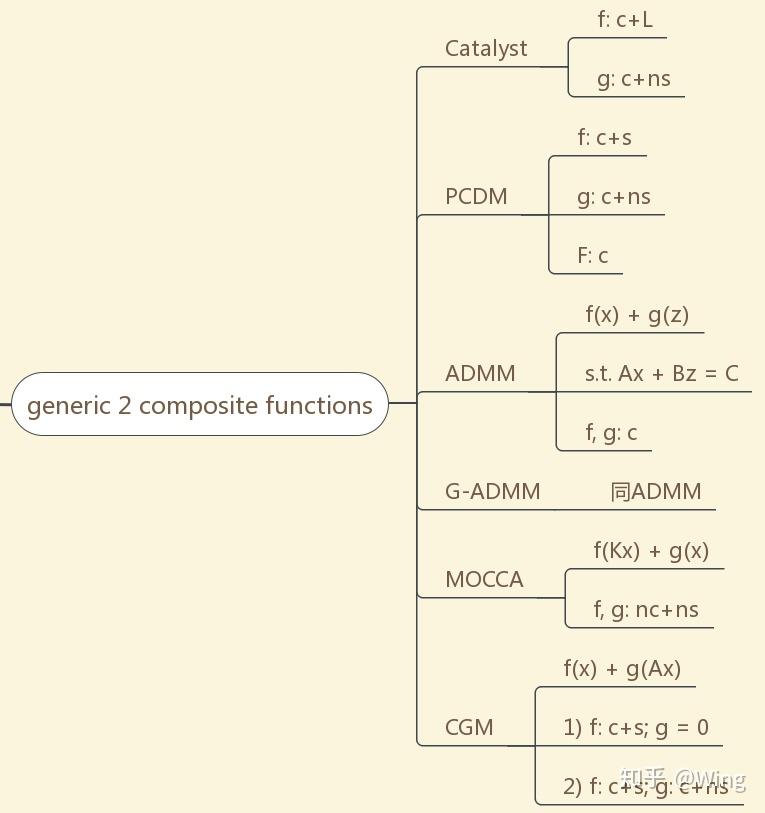
注:
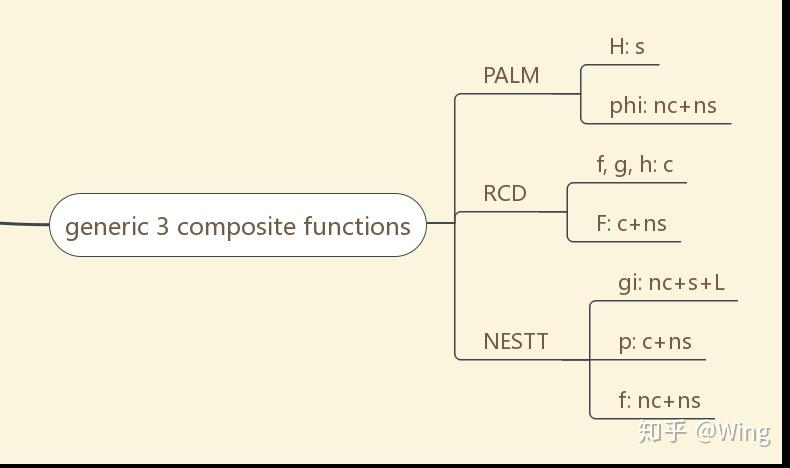
注:
The END.
声明:
1、欢迎转载,非学术水平,仅作为非专业交流使用。
2、此文的“主流”仅为个人见解,若有大佬认为疏漏了重要的算法,请留言指出~感谢!
3、思维导图所展示的算法适用的问题类型仅为部分论文内容,实际上以上算法的适用范围可能广泛得多,此处只是举出我所了解到的一隅,希望能有抛砖引玉之效。
