在神经网络结构设计中,我们经常会引入一些先验知识,比如ResNet的残差结构。然而我们还是用常规的优化器去训练网络。
在本工作中,我们提出将先验信息用于修改梯度数值,称为梯度重参数化,对应的优化器称为RepOptimizer。我们着重关注VGG式的直筒模型,训练得到RepOptVGG模型,他有着高训练效率,简单直接的结构和极快的推理速度。
官方仓库: RepOptimizer
论文链接: Re-parameterizing Your Optimizers rather than Architectures
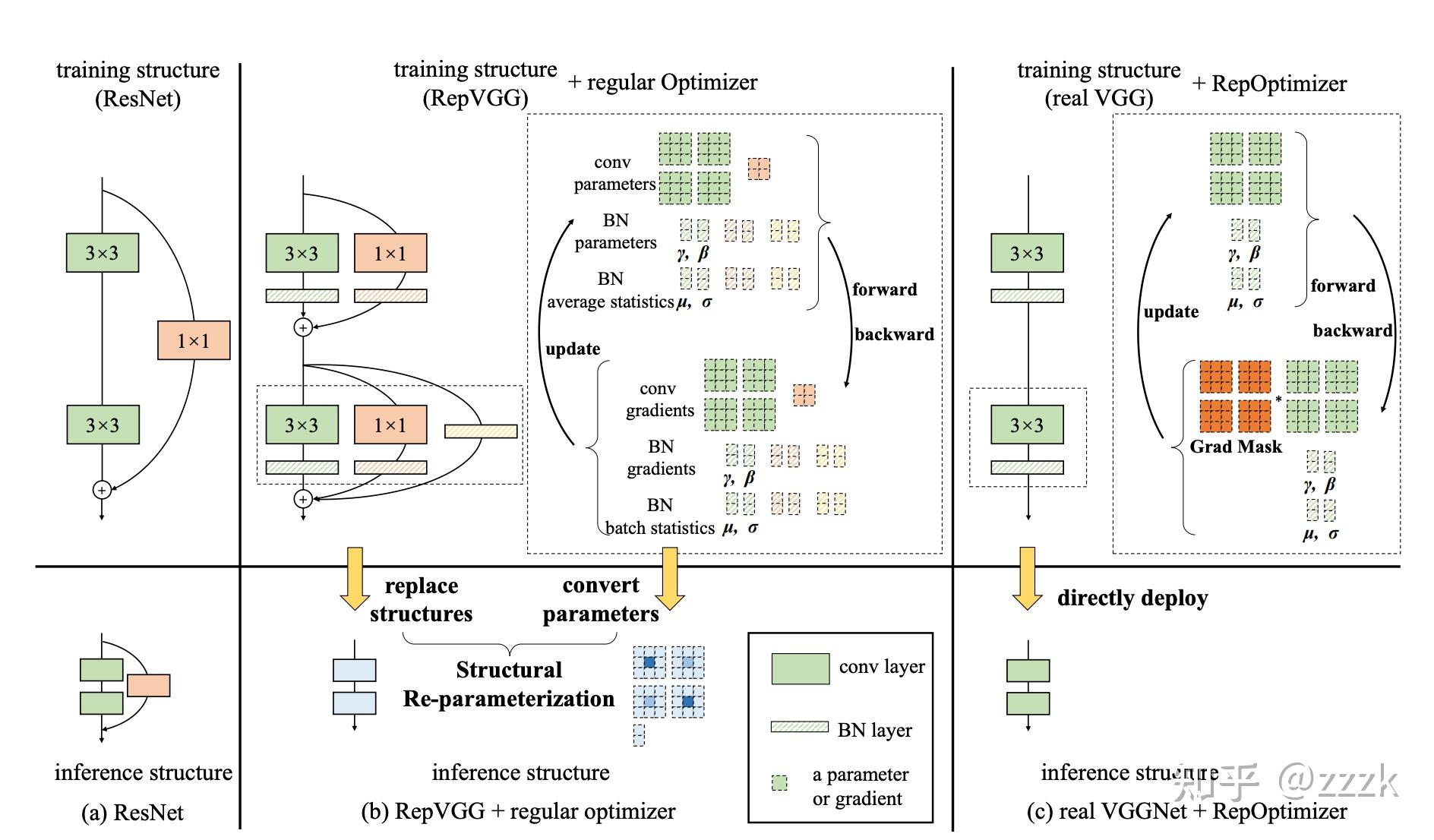
我们注意到一个现象,在特殊情况下,每个分支包含一个线性可训练参数,加一个常量缩放值,只要该缩放值设置合理,则模型性能依旧会很高。我们将这个网络块称为Constant-Scale Linear Addition(CSLA)
我们先从一个简单的CSLA示例入手,考虑一个输入,经过2个卷积分支+线性缩放,并加到一个输出中:
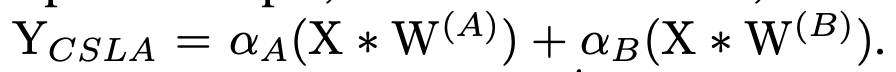
我们考虑等价变换到一个分支内,那等价变换对应2个规则:
融合的权重需为:
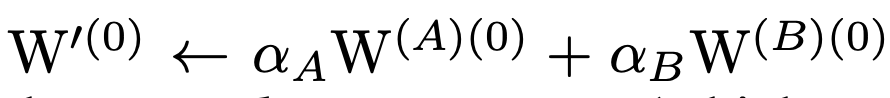
针对融合后的权重,其更新规则为:
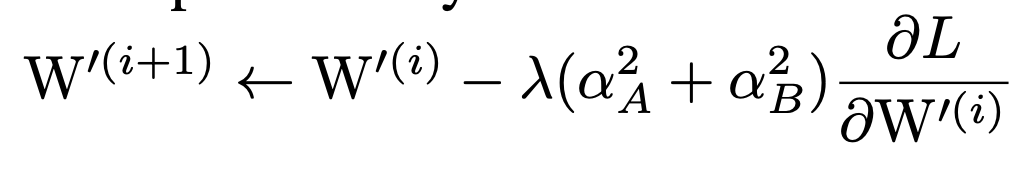
这部分公式可以参考附录A中,里面有详细的推导
一个简单的示例代码为:
import torch
import numpy as np
np.random.seed(0)
np_x=np.random.randn(1, 1, 5, 5).astype(np.float32)
np_w1=np.random.randn(1, 1, 3, 3).astype(np.float32)
np_w2=np.random.randn(1, 1, 3, 3).astype(np.float32)
alpha1=1.0
alpha2=1.0
lr=0.1
conv1=torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)
conv2=torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)
conv1.weight.data=torch.nn.Parameter(torch.tensor(np_w1))
conv2.weight.data=torch.nn.Parameter(torch.tensor(np_w2))
torch_x=torch.tensor(np_x, requires_grad=True)
out=alpha1 * conv1(torch_x) + alpha2 * conv2(torch_x)
loss=out.sum()
loss.backward()
torch_w1_updated=conv1.weight.detach().numpy() - conv1.weight.grad.numpy() * lr
torch_w2_updated=conv2.weight.detach().numpy() - conv2.weight.grad.numpy() * lr
print(torch_w1_updated + torch_w2_updated)
import torch
import numpy as np
np.random.seed(0)
np_x=np.random.randn(1, 1, 5, 5).astype(np.float32)
np_w1=np.random.randn(1, 1, 3, 3).astype(np.float32)
np_w2=np.random.randn(1, 1, 3, 3).astype(np.float32)
alpha1=1.0
alpha2=1.0
lr=0.1
fused_conv=torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)
fused_conv.weight.data=torch.nn.Parameter(torch.tensor(alpha1 * np_w1 + alpha2 * np_w2))
torch_x=torch.tensor(np_x, requires_grad=True)
out=fused_conv(torch_x)
loss=out.sum()
loss.backward()
torch_fused_w_updated=fused_conv.weight.detach().numpy() - (alpha1**2 + alpha2**2) * fused_conv.weight.grad.numpy() * lr
print(torch_fused_w_updated)
在RepOptVGG中,对应的CSLA块则是将RepVGG块中的3x3卷积,1x1卷积,bn层替换为带可学习缩放参数的3x3卷积,1x1卷积
进一步拓展到多分支中,假设s,t分别是3x3卷积,1x1卷积的缩放系数,那么对应的更新规则为:
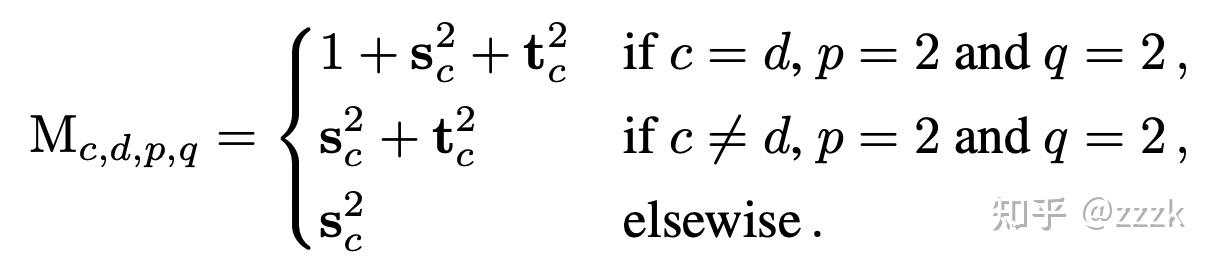
第一条公式对应输入通道==输出通道,此时一共有3个分支,分别是identity,conv3x3, conv1x1
第二条公式对应输入通道!=输出通道,此时只有conv3x3, conv1x1两个分支
第三条公式对应其他情况
需要注意的是CSLA没有BN这种训练期间非线性算子(training-time nonlinearity),也没有非顺序性(non sequential)可训练参数,CSLA在这里只是一个描述RepOptimizer的间接工具。
那么剩下一个问题,即如何确定这个缩放系数
受DARTS启发,我们将CSLA中的常数缩放系数,替换成可训练参数。在一个小数据集(如CIFAR100)上进行训练,在小数据上训练完毕后,我们将这些可训练参数固定为常数。
具体的训练设置可参考论文
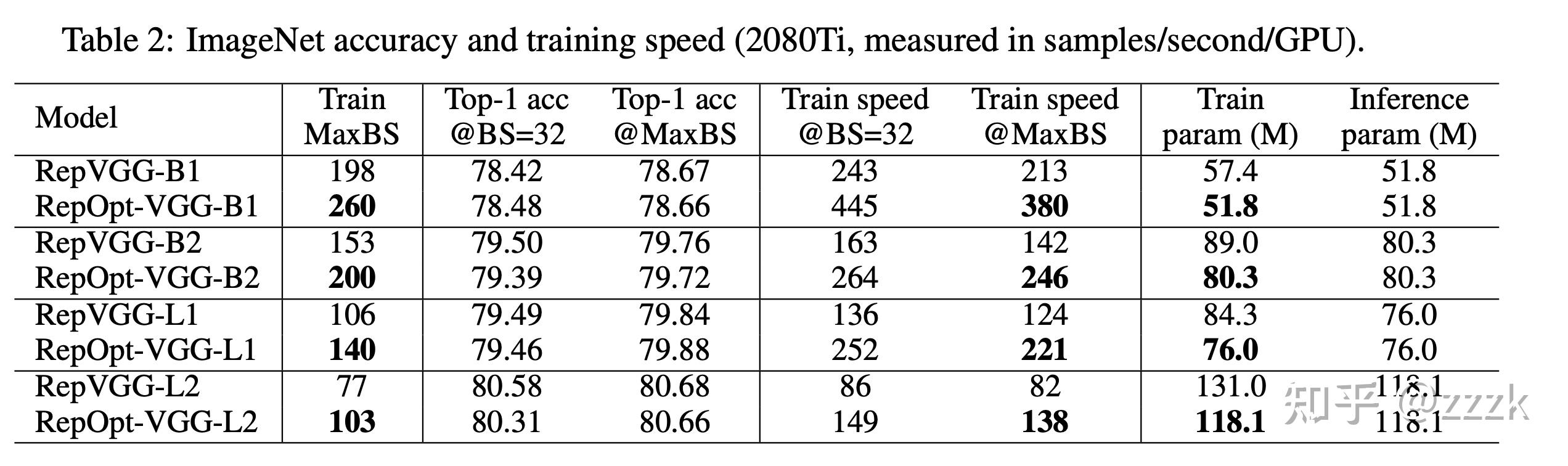
实验效果看上去非常不错,训练中没有多分支,可训练的batchsize也能增大,模型吞吐量也提升不少。
在之前RepVGG中,不少人吐槽量化困难,那么在RepOptVGG下,这种直筒模型对于量化训练十分友好:

我们主要看 repoptvgg.py 这个文件,核心类是 RepVGGOptimizer
在reinitialize 方法中,它做的就是repvgg的工作,将1x1卷积权重和identity分支给融到3x3卷积中:
if len(scales)==2:
conv3x3.weight.data=conv3x3.weight * scales[1].view(-1, 1, 1, 1) \\
+ F.pad(kernel_1x1.weight,[1, 1, 1, 1]) * scales[0].view(-1, 1, 1, 1)
else:
assert len(scales)==3
assert in_channels==out_channels
identity=torch.from_numpy(np.eye(out_channels, dtype=np.float32).reshape(out_channels, out_channels, 1, 1))
conv3x3.weight.data=conv3x3.weight * scales[2].view(-1, 1, 1, 1) + F.pad(kernel_1x1.weight,[1, 1, 1, 1]) * scales[1].view(-1, 1, 1, 1)
if use_identity_scales: # You may initialize the imaginary CSLA block with the trained identity_scale values. Makes almost no difference.
identity_scale_weight=scales[0]
conv3x3.weight.data +=F.pad(identity * identity_scale_weight.view(-1, 1, 1, 1),[1, 1, 1, 1])
else:
conv3x3.weight.data +=F.pad(identity,[1, 1, 1, 1])
然后我们再看下GradientMask生成逻辑,如果只有conv3x3和conv1x1两个分支,根据前面的CSLA等价变换规则,conv3x3的mask对应为:
mask=torch.ones_like(para) * (scales[1]** 2).view(-1, 1, 1, 1)
而conv1x1的mask,需要乘上对应缩放系数的平方,并加到conv3x3中间:
mask[:, :, 1:2, 1:2]+=torch.ones(para.shape[0], para.shape[1], 1, 1) * (scales[0]** 2).view(-1, 1, 1, 1)
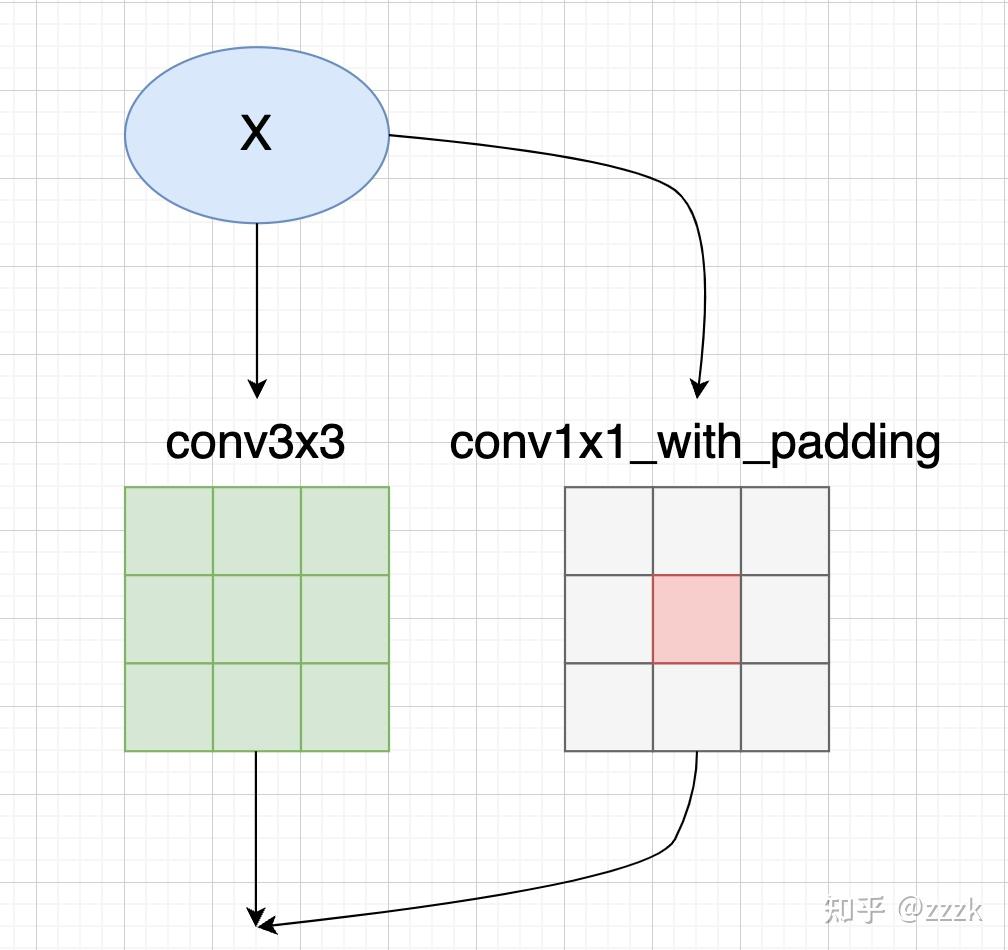
如果还有Identity分支,我们则需要在对角线上加上1.0(Identity分支没有可学习缩放系数)
mask[ids, ids, 1:2, 1:2]+=1.0
如果有不明白Identity分支为什么对应的是对角线话,可以参考下笔者的图解RepVGG
这篇文章出来有段时间了,但是好像没有很多人关注。在我看来这是个实用性很高的工作,解决了上一代RepVGG留下的小坑,真正实现了训练时完全直筒的模型,并且对剪枝友好,十分适合实际部署。
